文獻標識碼: A
文章編號: 0258-7998(2015)03-0101-04
0 引言
假設盲源分離的源信號個數為J,接收傳感器的個數為R,盲源分離可以分為超定盲源分離(J≥R)和欠定盲源分離(J<R)兩種情況。大多數盲分離算法都假設接收傳感器個數不少于源信號個數,然而在實際應用中,接收傳感器個數往往有限,有時會出現接收傳感器小于接收源信號個數的欠定混合情況(Underdetermined Blind Source Separation,UBSS)。欠定盲源分離一般分為兩步:(1)分離混合矩陣;(2)恢復源信號。本文只考慮對混合矩陣的估計。
針對欠定盲源分離問題,大多數文獻提出的算法是將觀測信號在時域或頻域稀疏化,這勢必會產生龐大的計算量,并且應用范圍局限于觀測信號和源信號數量較少的情況。考慮到源信號一般均滿足相互獨立和具有時間結構等特性,L.De Lathauwer提出了二階欠定盲辨識算法(Second-order Blind Identification of Underdetermined Mixtures,SOBIUM)[1],該方法不要求源信號在時域或變換域是稀疏的,通過對觀測信號的時延協方差矩陣組成三階張量直接進行平行因子分解實現對混合矩陣的估計。TICHAVSKY P在SOBIUM的基礎上提出了加權欠定混合矩陣盲分離算法[2],該算法通過加權張量分解來完成混合矩陣的估計,提高了分離信號的信干比,但是SOBIUM的迭代收斂時間較長,而且可能產生局部收斂。
針對以上問題,本文在SOBIUM方法的基礎上,加入了增強線搜索算法(Enhanced Line Search,ELS) 。ELS可以顯著改善最小二乘法的性能,降低局部收斂的風險,更重要的是減少了迭代次數,并且復雜度不高。
1 欠定盲分離與PARAFAC分解
1.1 瞬時欠定盲源分離模型
瞬時混合模型下的欠定盲源分離,其含噪混合模型為:
X(t)=AS(t)+N(t) t=1,…,T (1)
其中,X(t)=[x1(t),x2(t),…,xR(t)]T為R維接收信號矢量,A表示一個未知的J×R的混合矩陣,S(t)=[s1(t),s2(t),…,sR(t)]T為R維源信號矢量,N(t)=[n1(t),…,nR(t)]T為R維噪聲矢量,(*)T代表轉置。在噪聲不存在或者可以忽略不計的情況下,式(1)可以化簡為:
X(t)=AS(t)(2)
1.2 PARAFAC分解
平行因子(Parallel Factor,PARAFAC)分析又叫標準分解,是三面或更高面陣低秩分解的總稱。平行因子分解在多個應用領域發揮著有廣泛的作用,遠遠超出了化學計量學。平行因子分析在信號處理和通信領域中的數據域和子空間域[1-2]表現出良好的實用性,觀測數據被轉換為張量形式進行運算。下面給出關于平行因子的定義:
定義1:若矩陣A的任意kN個列線性獨立,則最大kN的值稱之為矩陣A的Kruskal秩,簡稱k秩。
定義2:如果一個張量X∈RI×J×K等于三個向量a,b,c的外積,則這個張量的秩為1。
定義3:一個三階張量X∈RI×J×K可以寫成秩為1的張量的最小數量的線性組合,叫作平行因子分解。這一最小數量(源信號數N)等于張量X的秩(可用于對源信號數的估計)即:
式中ar、br、cr分別代表矩陣A∈CI×R、B∈CJ×R和C∈CK×R的第r列。其中xijk=ai bj ck,i=1,…,I,j=1,…,J,k=1,…,K。
平行因子分解的矩陣模式可以寫為:
X(1)=(B⊙C)AT,X(1)∈CJK×I
X(2)=(C⊙A)BT,X(2)∈CKI×J
X(3)=(A⊙B)CT,X(3)∈CIJ×K(4)
平行因子的唯一性在文獻[3-5]中進行了研究,可以總結為下面的定理:
定理1:如果滿足
kA+kB+kC≥2R+2(5)
則平行因子分解唯一。kA、kB、kC分別代表矩陣A、B、C的秩。R為源信號的個數。
用平行因子分解解決欠定盲分離混合矩陣問題時,源信號個數J與接收傳感器最大個數Rmax的關系如表1所示。

1.3 PARAFAC分解估計欠定混合矩陣
若源信號為零均值且互不相關的非平穩信號,那么源信號在t時刻的二階自相關矩陣可表示為:
式中DN=Est s■■是塊對角陣,n=1,…,N,N是分塊的個數,矩陣A稱為分塊成型矩陣。式(3)中時間延時?子n可以為零,上標T表示轉置。
將矩陣組{RN}轉為(d,d,M)維的三階張量形式:
其中θ代表一個影響矩陣A和D的所有元素的參數向量。![7GH1GV}37L67JY$S{P]TKYM.png 7GH1GV}37L67JY$S{P]TKYM.png](http://files.chinaaet.com/images/2017/01/11/6361973134115400008951315.png)
式中R代表張量,R為源信號的數目,⊙表示張量的外積,{an}和{dn}分別為A和D的列向量,上標*代表共軛轉置。
2 加權增強最小二乘法
2.1 交替最小二乘法算法
張量的標準分解通常使用三線性交替最小二乘(Alternating Least Squares,ALS)算法實現。迭代過程中的代價函數為:
||·||F表示Frobenius矩陣范數。ALS的目標是在每一步迭代中,使張量R與它的當前估計值的差的范數最小。用于平行因子分析模型擬合的 ALS 過程即在固定上次迭代獲取的部分矩陣估計值基礎上, 估計其他矩陣, 該交錯映射形式的最小二乘回歸過程循環下去, 直至收斂。矩陣A、B和C的估計可以表示為:
其中上標“+”代表Moore-Penrose偽逆。
2.2 增強的線搜索(ELS)
通常在數據量非常大,或當兩個因素幾乎共線時,ALS的收斂性是非常緩慢的[6]。壓縮和線搜索是應對收斂慢問題的兩種解決方案。本文采用增強線搜索來加快ALS: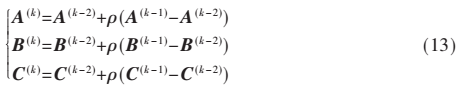
上式中上標(k)、(k-1)、(k-2)分別代表第k次,第k-1次,第k-2次迭代。令:
其中![S2~VCV@MIRA]IXAHDH(MOTS.png S2~VCV@MIRA]IXAHDH(MOTS.png](http://files.chinaaet.com/images/2017/01/11/6361973203003100007315109.png) 代表迭代的方向。松弛因子?籽表示迭代的步長。?籽的選擇十分重要。同一個算法只改變?籽的值,迭代收斂的速度變化如圖1所示。
代表迭代的方向。松弛因子?籽表示迭代的步長。?籽的選擇十分重要。同一個算法只改變?籽的值,迭代收斂的速度變化如圖1所示。
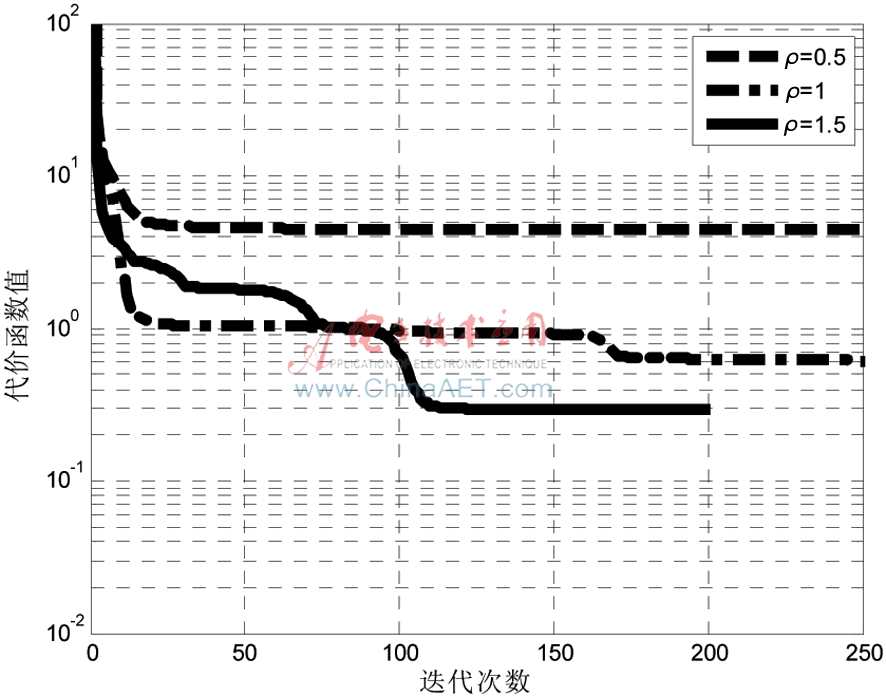
圖1 松弛因子?籽對迭代收縮的影響
2.3 平行因子的增強加權目標函數
平行因子分解模型同獨立分量分析模型一樣,具有置換不確定性和排列不確定性。為了有效地解決這個問題而不犧牲算法的收斂性,本文采用如下收斂函數:![1$@YGOESBUYOH~0U0L`]R[G.png 1$@YGOESBUYOH~0U0L`]R[G.png](http://files.chinaaet.com/images/2017/01/11/6361973210138100009786548.png)
其中 隨著迭代次數的增加?著趨于0。I表示與XJK×I相同維數的單位矩陣。式(15)可以寫為:
隨著迭代次數的增加?著趨于0。I表示與XJK×I相同維數的單位矩陣。式(15)可以寫為: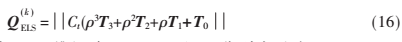
其中JK×I維矩陣T3、T2、T1和T0分別表示為:![EKN]56~OW0CEAQ1)C9MWY)T.png EKN]56~OW0CEAQ1)C9MWY)T.png](http://files.chinaaet.com/images/2017/01/11/6361973224782900005675876.png)
上標k和k-2為了簡便已省略。定義Vec為矩陣矢量化符號,例如有矩陣A∈CI×J,則:![QP1]O8TPS5{G@O_H2O2PZ0L.png QP1]O8TPS5{G@O_H2O2PZ0L.png](http://files.chinaaet.com/images/2017/01/11/6361973228942300002239262.png)
則等式(16)等效于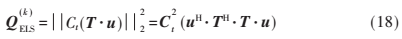
其中4×1維矢量![`M`YJ]SP8M3Z95)RK@@~34L.png `M`YJ]SP8M3Z95)RK@@~34L.png](http://files.chinaaet.com/images/2017/01/11/6361973239807000006698411.png) 代表共軛轉置,式(18)對于復數和實數都適用[7]。IJK×4維矩陣T分別由T3、T2、T1和T0的列矢量組合而成,可以表示為:
代表共軛轉置,式(18)對于復數和實數都適用[7]。IJK×4維矩陣T分別由T3、T2、T1和T0的列矢量組合而成,可以表示為:
3 數據實驗:分離混合語音的混合矩陣
本節通過數值仿真實驗對本文算法(SO-WALS-ELS)與SOBIUM算法的性能做比較。混合矩陣估計的相對誤差公式為:
其中,![U$9(NK]AHEE5Z_F747H]C[3.png U$9(NK]AHEE5Z_F747H]C[3.png](http://files.chinaaet.com/images/2017/01/11/6361973617379000003331161.png) 。假設它們的列向量均已單位化且消除了排列順序的不確定性。
。假設它們的列向量均已單位化且消除了排列順序的不確定性。
實驗中采用4路獨立源信號混合成3路觀測信號為例,4路語音從語音庫中隨機選取,采樣率為16 kHz,取160 000點,混合方式為瞬時混合,H為混合矩陣。圖2為源信號,圖3為混合信號,圖4為分離信號,圖5為本文算法與SOBIUM算法的對比圖。
圖2 源信號

圖3 混合信號

圖4 分離信號
從圖2~圖5可以看出,改進的算法分離出了大概原始信號,但分離信號的順序和極性都發生了變化,這也是目前平行因子分解尚無法解決的問題。![``(V6D5~UPJ}NY]5Y5UPI10.png ``(V6D5~UPJ}NY]5Y5UPI10.png](http://files.chinaaet.com/images/2017/01/11/6361973627631100001718278.png)
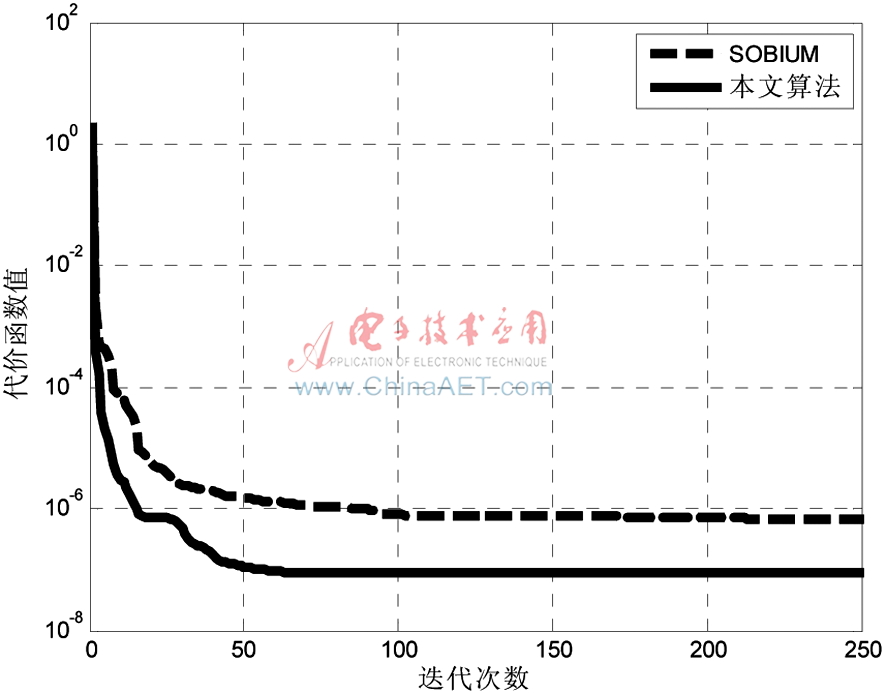
圖5 本文算法與SOBIUM算法的對比圖
![RG_M7DFZ8$2VM3{CP@]EKWF.png RG_M7DFZ8$2VM3{CP@]EKWF.png](http://files.chinaaet.com/images/2017/01/11/6361973631380400001348155.png)
根據公式,改進前的算法相對誤差為0.055 9,改進后的相對誤差為0.029 8。經過多次實驗,改進后的方法比原方法具有更快的收斂速度,并且更精確。
4 結論
本文提出了一種基于增強加權最小二乘法的欠定混合矩陣分離的新算法,適用于非平穩信號。首先,該算法將接收信號的空間協方差矩陣疊加成三階張量,然后再對此三階張量進行平行因子分解,最后利用增強加權最小二乘法完成混合矩陣估計。仿真實驗結果表明:本文提出的算法具有比SOBIUM算法更好的分離效果和更好的魯棒性,而且實現簡單,可滿足實際應用的要求。
參考文獻
[1] LIEVEN De LATHAUWER.Blind identification of underde-termined mixtures by simultaneous matrix diagonalization[J].IEEE Transactions on Signal Processing,2008,56(3):1096-1105.
[2] PETR Tichavsky,ZBYNEK Koldovsky.Weight adjusted tensor method for blind separation of underdetermined mixtures of nonstationary sources[J].IEEE Transactions on Signal Processing,2011,59:1037-1047.
[3] KRUSKAL J B.Three-way arrays:Rank and uniqueness of trilinear decompositions,with application to arithmetic complexity and statistics,Linear Algebra Appl.,1977(18):95-138.
[4] STEGEMAN A,SIDIROPOULOS N D.On kruskal’s uniqueness condition for the Candecomp/ PARAFAC decomposition[C].Linear Algebra and its Applications,2007
(420):540-552.
[5] NICHOLAS D.SIDIROPOULOS,RASMUSBRO.On the Uni-queness of Multilinear Decomposition of N-way Arrays[J].J.Chemometrics,2000,14(3):229-239.
[6] RAJIH M,COMON P,HARSHMAN R A.Enhanced line search:A novel method to accelerate PARAFAC[J].SIAM Journal on Matrix Analysis,2008,30(3):1148-1171.
[7] NION D,DE LATHAUWER L.Line Search computation of the Block Factor Model for blind multi-user access in wireless communications[C].Advances in Wireless Communi-cations(SPAWC) France,Cannes,.IEEE Workshop on Signal Processing,2006.
[8] NION D,DE LATHAUWER I.An enhanced line Search scheme for complex-valued tensor decompositions.Application in DS-CDMA[J].Signal Processing,2008,3(88):749-755.

