杜青
(南京工程學院 計算機工程學院,江蘇 南京 211167)
摘要:本文以C++語言設計了大整數類,在類中以數組存儲大整數,同時借鑒分治算法思想實現了大整數的乘法運算。算法中將被乘數與乘數按照相同位數進行分組,通過對每組較小數值整數進行乘法和加法運算而得到大整數相乘的積。該程序在VC++2015開發平臺調試通過。測試結果表明,當每個分組數據位數多時,運算速度顯著提高。
關鍵詞:大整數;大整數相乘;分治算法;類
中圖分類號:TP301文獻標識碼:ADOI: 10.19358/j.issn.1674-7720.2017.02.003
引用格式:杜青.基于類的大整數乘法運算的實現[J].微型機與應用,2017,36(2):8-9,13.
0引言
大整數是指數值很大、超出計算機整數表達和處理范圍的非負整數。一般計算機能夠處理的整數有三種類型,即2字節(16 bit)、4字節(32 bit)和8字節(64 bit)整數,其中8字節整數取值范圍最大,8字節無符號整數取值范圍是:0~264-1。當整數值超過整數范圍的最大值264-1時,計算機無法直接處理。
大整數的乘法運算在密碼學等領域有著廣泛的應用。如著名的公鑰加密算法RSA算法,大整數相乘是其中必不可少的運算,由于運算中使用的密鑰推薦位數為1 024位,為了達到更高安全級別,密鑰長度甚至達到上萬位,遠遠超出計算機所能直接處理的64 bit的整數范圍。
當需要對大整數進行乘法運算時,面臨的問題是:如何存儲大整數以及如何提高大整數乘法的運算速度。已有的實現大整數乘法的程序中,有的采用累加的方式,將被乘數重復相加若干次,累加的次數等于乘數;有的按照手算的形式,將乘數逐位與被乘數相乘,并將結果做位移運算后按位求和[1]。當被乘數與乘數位數很多時,這些方法運算時間長。
本文以C++語言設計了一個大整數類,在類中以數組存儲大整數,同時借鑒分治算法的思想[2],將數值很大的大整數分解為若干組數值較小的整數,通過對每組較小數值整數的運算得到大整數相乘的積。程序在VC++2015開發平臺調試通過。
1大整數的存儲
由于大整數位數多,若用字符串形式表示,在做運算時,首先要將表示大整數的字符串轉換成數值。轉換時考慮到大整數的數值一般超出整數的取值范圍,所以采用整型數組存儲其值[3]。
以下給出了大整數類BigInt的聲明,類中的數據成員uint64_t 類型數組array用于存放大整數,uint64_t是64 bit無符號整數類型。轉換時從大整數字符串最低位開始,每K個字符為一組,最高位不足K個字符時補0,將每組字符轉換為一個數值較小的整數,每個較小整數存放到整型數組的一個元素中。類中數據成員n為已存放了數據的元素個數,即分組數。類聲明代碼如下:
#define N 10000//數組大小
#define K 3//每個分組中包含的字符個數
class BigInt
{public:
BigInt();//無參構造函數,將n置0
BigInt(string str);//轉換構造函數
int compare(BigInt num); //比較類對象大小
friend BigInt operator*(BigInt num1, BigInt num2);//重載乘法運算符
friend int operator>(BigInt num1, BigInt num2);
//重載大于運算符
private:
uint64_t array[N];//存放大整數的數組
int n;//存放了數據的元素個數
};
類中的轉換構造函數實現了將大整數字符串分組,并將各組字符串轉換為數值存放到array數組中的操作。轉換構造函數的代碼如下:
BigInt::BigInt(string str) //將字符串轉換為數值
{int end = str.length() - 1, i;
uint32_ttemp,w;//w代表權重
n = 0;
i = end;//從最低位開始處理
while (i >= 0)
{temp = 0;w = 1;
for (int k =0;k<K;k++) //K個字符組成1個數
{if (str[i] >= 0&&str[i] <= 9)
{temp = temp + w*(str[i] - 0);
w *= 10; i--;
if (i<0)break;
}
}
array[n] = temp;n++;
}
for (i = n;i<N;i++) array[i] = 0; //其他元素置0
}
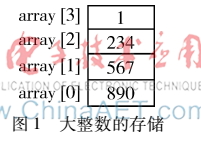
當K=3時,字符串“1234567890”在數組array中存放的形式如圖1所示。
2大整數乘法的實現
2.1大整數乘法的算法
當一個m位的大整數X與一個n位的大整數Y相乘時,如按照手算的方式進行計算,需要將Y的每一位與X的每一位相乘,共要做m×n次數據相乘。如m、n很大,則數據相乘次數多,從而使整個乘法運算時間長。
為了解決這個問題,利用分治法的思想,將X、Y均分解為K位一組的整數[4],即X分解為…xi…x2x1x0,共(m+K-1)/K組數字,Y分解為…yj…y2y1y0,共 (n+K-1)/K組數字,運算時將由Y分解得到的每一組整數yj與由X分解得到的每一組整數xi相乘。
以K=3時,1234567890與1234567890做乘法運算為例,如按手算方式進行運算,需做10×10共100次數據相乘,而若將被乘數與乘數分解為3位一組的數字,即各自分解為4組數字,如圖2所示,則只需要完成4×4共16次數據相乘,數據相乘次數大大減少。在進行分組數據相乘后,再按組進行數據相加,從而得到兩個大整數乘法運算的積。大整數分組運算過程示意圖如圖2所示。

當K較大時,每組數據因位數增加而數值變大,分組數目隨之減少,分組數據乘法次數也減少。但當K過大時,每組數據與其他組數據相乘時得到的中間結果可能會超出整型數據的最大值而導致數據溢出。為了防止溢出情況的出現,K的取值不能太大。由于uint64的最大值是264-1,因此每組數字的最大值不能超過232-1,即4 294 967 295,由此推斷,每組數字不能超過9位,即K要滿足:1≤K≤9。
2.2大整數乘法的實現
m位的大整數X與n位的大整數Y進行乘法運算時,將yj依次與xi相乘,保留xi*yj%BASE為中間結果,yj*xi/BASE為進位,其中BASE的值等于10K,是運算的基[5]。兩個大整數相乘后得到的乘積的位數是m+n或m+n-1[6]。
下面給出了實現大整數乘法運算的函數定義,該函數是乘法運算符重載函數,已在BigInt類中聲明為友元。該函數代碼如下:
#define BASE 1000 //運算的基
BigInt operator*(BigInt num1, BigInt num2)
{BigInt temp1, temp2;
if (num2>num1)//保證被乘數大于乘數
{temp1=num1; num1=num2; num2=temp1;}
uint64_t num, c;//num存放中間結果,c為進位
int maxi, mini, i, j;
maxi = num1.n; //被乘數分組數
mini = num2.n; //乘數分組數
for (i = 0;i<mini;i++)
{c = 0;//進位初值為0
for (j = 0;j<maxi;j++)
{num = num1.array[j] * num2.array[i] + c;
temp2.array[j+i]+=num%BASE; //做一次
//分組相乘之后做分組加法
c = num / BASE;
if (temp2.array[j + i] >= BASE)//判斷是
//否超出BASE
{temp2.array[j+i]=temp2.array[j+i]%BASE;
c++;//進位加1
}
}
if (c) temp2.array[j + i] += c; //有進位時
}
temp2.n = maxi + mini - 1;//設置乘積的分組數
if (c) temp2.n++; //最后一次運算有進位時
return temp2;
}
以上實現大整數乘法的函數中,做一次分組數據相乘之后,將得到的中間結果做分組加法運算,并且在做分組加法運算時,要判斷加法運算的結果是否溢出,若溢出,將加法運算結果對BASE取余數,同時進位加1。
2.3運行測試
在VC++2015開發平臺運行程序,測試時用兩個4 000位大整數做乘法,且使該乘法運算重復執行1 000次,測試當K取1、2、3、……、9不同值時所花費時間,得到結果如表1所示。由表1可以看出,K值增大,大整數乘法運行時間大大減少。

3結論
本文以C++類的方式實現了大整數的乘法運算,算法中根據分治法思想,將被乘數與乘數按照相同位數進行分組,通過對每組較小數值整數進行運算,從而得到大整數相乘的結果。該程序在VC++2015開發平臺調試通過。實驗結果表明,當每個分組數據位數多時,乘法運算速度顯著提高。
參考文獻
[1] 周健,李順東,薛丹.改進的大整數相乘快速算法[J].計算機工程,2012,38(16):121-123.
[2] 王曉東. 計算機算法設計與分析(第3版)[M]. 北京:清華大學出版社, 2014.
[3] 楊燦,桑波.大整數乘法運算的實現及優化[J].計算機工程與科學,2013,35(3):183-190.
[4] 王念平,金晨輝.用分治算法求大整數相乘問題的進一步分析[J].電子學報,2008,36(1):133-135.
[5] 李文化,董克家.大整數精確運算的數據結構與基選擇[J].計算機工程與應用,2006,42(32):24-26.
[6] 劉覺夫,周娟.大整數運算的基選擇[J].華東交通大學學報,2007,24(2):100102.

