代曦,李騫,顧大權,黃巖
(解放軍理工大學 氣象海洋學院,江蘇 南京 211101)
摘要:等值線編輯是對各形勢場等值線自動化分析結果的人工修正,是對提取準確等值線結果的必要補充。針對已有等值線交互編輯方法難以滿足不相交約束、操作復雜等問題,提出一種基于拉普拉斯坐標系的等值線交互編輯方法。實驗結果表明,編輯結果有效保持了原有等值線的形狀拓撲,且人工操作更少,可滿足業務應用中等值線交互編輯需求。
關鍵詞:等值線; 三角剖分;拉普拉斯
0引言
*基金項目:國家自然科學基金項目資助(41305138,41174164)等值線是將數據某一數量指標值相等的各點連成的平滑曲線,它具有連續性、不相交等特點。現有等值線分析主要分為手工分析和軟件自動分析兩種,其中手工分析相對復雜、耗時較長,但此方法優勢在于可融合預報人員經驗與其氣象要素信息;自動分析采用網格追蹤等方法對格點數據進行跟蹤,分析速度快,但與手工分析結果存在一定差距,不能很好地滿足業務需求。當前大多數可視化及氣象分析軟件已實現等值線的自動分析功能,SURFER、Micaps、Grads、MATLAB、ARCGIS、Tecplot等均有等值線分析模塊[12]。上述系統的主要問題表現在:訂正結果不能滿足等值線網格局部的拓撲結構需求;修正等值線時容易出現等值線相交的情況;只能實現對單條等值線進行修改,如對多條線進行修改,需要反復操作,效率低。
針對上述問題,本文提出了一種基于拓撲結構的等值線修正方法。首先對已有的等值線數據進行三角剖分,依據剖分結果識別等值線間的拓撲關系,并對剖分結果建立Laplacian坐標系[34]。然后由用戶交互輸入修改意圖,在交互修改過程中通過Laplacian坐標對等值線修改移動部分進行約束,同時通過笛卡爾坐標約束固定點,通過最小二乘法求解移動點和固定點雙重約束下的線性系統,從而重新修改移動點[56]。通過上述方法,可以實現在保持等值線集合拓撲結構的前提下對等值線進行修改。
本文提出方法的流程如圖1所示。

1三角剖分
三角剖分是計算機輔助幾何設計、幾何造型及計算機圖形學中研究的重要內容之一。本文將等值線集合進行離散化并對得到的離散點進行三角剖分得到三角網格。目前,三角剖分可以通過動態規劃[7]和德勞內三角剖分算法[8]實現,但動態規劃算法主要是通過計算最短邊來排除病態的三角網格。而在等值線族中,由于等值線彎曲變化,部分等值線在某一個區域內較為集中,通過動態規劃算法來實現三角剖分可能丟失等值線間的拓撲關系。因此,本文采用德勞內三角剖分算法。其主要流程如圖2所示。
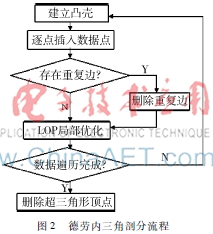
首先建立凸殼,包含了所有的離散點,然后向其中插入一點,該點與包含它的三角形三個頂點相連,形成三個新的三角形,然后逐個對它們進行空外接圓檢測,同時用Lawson設計的局部優化過程LOP進行優化,即通過交換對角線的方法來保證所形成的是Delaunay三角網。
2拓撲結構識別與Laplacian坐標系建立
Laplacian坐標表示方法又稱為微分坐標方法或δ坐標[9],或局部平均曲率法線。在網格頂點處應用Laplacian算子,可用于表征局部曲面的幾何特征。建立拓撲結構后,將笛卡爾坐標系轉換為差分的拉普拉斯坐標系。主要針對修改范圍內的點,為下一步能量方程求解提供依據。
根據設定的修改范圍,從用戶選中的坐標點出發,廣度搜索出一系列鄰接點,根據差分坐標公式求出每點的δ坐標。得到的坐標存儲在鏈表中。本文為了建立拉普拉斯坐標系進行如下定義:
(1)拉普拉斯網格

μ表示已知的N個點組成的三角網格。V表示節點,E表示邊,F表示平面。每個i∈μ表示笛卡爾坐標系中的節點用vi=(xi,yi,zi)表示。
首先通過中心和與它直接相連的節點定義差分坐標系:

其中,N(i)={j|(i,j)∈E},表示與i節點相鄰節點的個數。
從絕對笛卡爾坐標系到差分坐標系的轉換可以表示為一個矩陣:

令D是一個對角陣,Dii=di,矩陣從絕對坐標系轉換到關系坐標系:
L=I-D-1A(4)
定義:
Ls=DL=D-A(5)
那么,

Lsx=Dδ(x),Lsy=Dδ(y),Lsz=Dδ(z)
其中x是n個向量包含x的絕對坐標的所有頂點。
矩陣Ls被稱為拓撲拉普拉斯網格。圖形表示的拉普拉斯廣泛地應用在代數和圖形學原理中,最主要的原因是因為它的代數特性能很好地與圖形表示相結合。從差分幾何角度來看,δ坐標系被視作離散化的連續拉普拉斯貝爾特拉米算子。

(2)三維仿射變換
常見的三維變換包括平移變換、旋轉變換、縮放變換、反射變換和錯切變換。若取齊次坐標來表示三維空間中的點,三維變換可表示為4×4的變換矩陣。
記(Tx,Ty,Tz)為平移向量, 繞x軸旋轉θ角的旋轉變換矩陣為:

同樣可以獲得繞y軸、z軸旋轉的變換矩陣。縮放矩陣為:
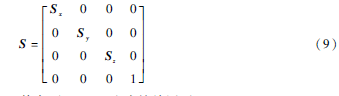
其中,(Sx,Sy,Sz)為縮放因子。
3能量方程的求解
通過網格模型的笛卡爾坐標構造其Laplacian坐標。由于變換矩陣L(或Ls)為奇異矩陣[10],不存在可逆矩陣,因此不能使用V′=L-1δ重建模型。
由于Laplacian坐標存在平移不變性,因此變換矩陣L的秩為n-1。為了能夠唯一地重構笛卡爾坐標系中的網格模型,需要求解一個滿秩的線性方程組,因此需要指定更多的變形特征頂點的笛卡爾坐標為約束條件。令空間中位置已知頂點的索引值集合為C,有|C|個位置約束的形式為:
V′j=cj,j∈C
如果記C={1,2,...,m},則需要求解的線性方程組表示如下:

方程組中的系統矩陣記為Lo。在本文中,使用公式作為位置約束條件(或稱為模型約束條件)。權值ω>0可以用來調整位置約束條件的重要性,每個約束都應該有相應的權值,可以在Laplacian矩陣上針對不同行使用不同的權值。附加的屬性約束條件使線性方程組成為超定方程組,因此基本上沒有完全精確的解,可通過最小二乘法求解近似解,當系統滿秩時就存在唯一解:

式(11)的第一項表示盡可能保持原始網格的Laplacian坐標不變,第二項表示盡可能減少特征頂點處的誤差。求解值的精確度與現行方程組的約束條件有很大關系。
基于線性邊約束的網格編輯方法在模型重建時,通過最小二乘系統求解獲得的模型為近似解。當模型集合細節特征較復雜時,一次求解不一定能獲得較高質量的變形效果,需要多次迭代求解,逐漸逼近精確值。
4實驗結果與分析
為了驗證方法的可行性,本文分別使用仿真數據和2011年數據庫中選取的4月20日12時的全球等壓線數據進行了實驗。仿真數據為16條平行線,共510個采樣點。全球等值線數據共有682條等值線,19 985個采樣點。
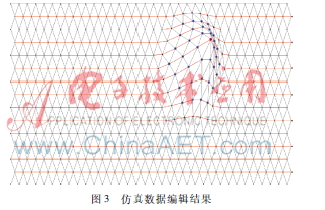
圖3仿真數據編輯結果通過上文提到的兩個過程,用戶交互編輯修改點,使其帶動修改范圍內的點一起移動,從而達到修改的效果,實驗結果如圖3。其中用戶交互修改的點只有淺色的點,深色的點均根據淺色點移動而改變位置,從而達到等值線修改范圍內自動編輯的要求。
本文對全球數據的局部進行編輯實驗,根據修改范圍不同編輯結果如圖4。圖4的修改范圍為2個網格。

從實驗結果可以看出,不同的修改范圍得到的數據編輯結果是不同的。最后本文對全球數據進行了編輯實驗,如圖5所示。其中用戶選擇的修改范圍在左下角。
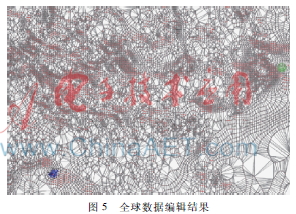
實驗結果證明,采用本文方法對等值線數據進行局部自動修正是可行性的。
參考文獻
[1] 王軟宏. 等值線的自動繪制方法及在計算機上的實現[D].吉林:吉林大學數學研究所,2003.
[2] 中國氣象局.MICAPS3.2 用戶使用手冊[Z]. 2012.
[3] SORKINE O, LIPMAN Y, COHENOR D, et al. 2004.Laplacian surface editing[C]. In SGP′04: Proceedings of the 2004 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, ACM, New York, USA:175184.
[4] LIPMAN Y, SORKINE O, COHENOR D, et al. Differential coordinates for interactive mesh editing[C]. In Proceedings of Shape Modeling International (2004), IEEE Computer Society Press:181190.
[5] BOTSCH M, BOMMES D, KOBBELT L. Efficient linear system solvers for mesh processing[J]. IMAMathematics of Surfaces XI, Lecture Notes in Computer Science,2005,3604:6283.
[6] FLOATER M S. Mean value coordinates[J]. Computer Aided Geometric Design, 2003,20(1):1927.
[7] 劉晶, 張九龍, 李曄, 等. 基于圖像不變特征與三角剖分的水印算法[J]. 西安理工大學學報, 2009, 25(2): 227230.
[8] 余杰, 呂品, 鄭昌文. Delaunay 三角網構建方法比較研究[J]. 中國圖象圖形學報, 2010, 15(8): 11581167.
[9] 許斌,李忠科,宋大虎.基于支持向量機的 Laplacian 網格曲面孔洞修補算法[J].計算機工程與設計, 2014, 35(1): 237242.
[10] 王勇.基于流形學習的分類與聚類方法及其應用研究[D].長沙:國防科學技術大學, 2011.

