摘 要: 時間序列的維數比較大,直接對時間序列進行聚類性能不理想。如何提高時間序列的聚類性能,是主要研究點。首先使用鄰域保持嵌入對時間序列樣本維數約簡,然后對維數約簡后的數據進行聚類融合,最后將它的聚類性能與已有方法如主成分分析、分段聚合近似進行比較。實驗表明,所提出的算法更能提高聚類性能。
關鍵詞: 時間序列;聚類融合;維數約簡;鄰域保持嵌入
0 引言
時間序列是一種高維且隨著時間變化而變化的數據。時間序列聚類在風險管理、車輛檢測[1]、隧道通風控制、交通流等領域廣泛應用。
蘇木亞等人[2]提出了基于主成分分析(Principal Component Analysis,PCA)的時間序列聚類方法,但是PCA是線性方法,現實數據集往往具有非線性特征;李海林等人[3]先用分段聚合近似(Piecewise Aggregate Approximation,PAA)對時間序列降維,然后進行聚類,但是PAA沒有考慮樣本之間的內在關系。鄰域保持嵌入(Neighborhood Preserving Embedding,NPE)[4]是局部線性嵌入(Locally Linear Embedding,LLE)[5]的線性近似,它清晰地考慮了數據的流形結構,約簡后的數據可以最優地保持原數據集的局部鄰域信息,并考慮了樣本之間的內在關系。
針對單一聚類算法存在結果不穩定的問題,現在趨向于融合多個聚類的結果,即聚類融合。本文提出了一種基于NPE的時間序列聚類融合算法,實驗結果表明,本文提出的算法與已有方法相比,更能提高聚類性能。
1 背景
1.1 鄰域保持嵌入
設原始數據集X={x1,x2,…,xn}?奐Rl,NPE[4]找到變換矩陣A。使用A將X映射到Y={y1,y2,…,yn}Rd,(d<<l),能夠保持X的局部結構。
(1)構造鄰域圖G。如果xj在xi的k近鄰中,就在兩個點之間放一條有向邊。
(2)計算加權矩陣W。通過解決最小化問題得到點xi到xj之間邊的權重Wij;如果xi與xj之間沒邊,則Wij=0。

其中,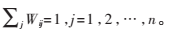
(3)計算映射。通過解決一般特征值問題來獲得轉換向量a:
XMXTa=λXXTa(2)
其中,X=(x1,…,xn),M=(I-W)T(I-W),I=diag(1,…,1)。假設A=[a0,a1,…,ad-1],特征值排序后為0≤λ0≤…≤λd-1。得到y:yi=ATxi,其中yi是d維向量,A是l×d矩陣。
1.2 基于互信息的聚類成員的權值
聚類成員Pa、Pb類標記用{P1a,P2a,…,Pka}和{P1b,P2b,…,Pkb}表示。設Pia中有ni個元素,Pjb中有nj個元素,Pia和Pjb中相同元素有nij個。互信息ФMI為[6]:
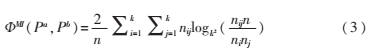
每個聚類成員的平均互信息為:
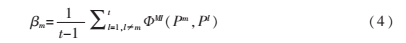
βm越大,聚類成員Pm所包含的特有信息就越少,其權值[6]可定義為:

其中,Z是對權值標準化,wm>0且
2 時間序列聚類融合算法
算法包括三步:首先,使用NPE對數據集進行維數約簡;其次,對降維后的數據進行聚類,產生聚類成員;最后,使用加權投票法進行聚類融合。
聚類融合算法如下:
輸入:數據集Data,近鄰個數k,嵌入維數d,聚類個數M,聚類成員個數H
輸出:聚類結果
(1)使用PCA對數據集進行預處理;
(2)yi←APCATxi,其中,APCA是PCA的轉換矩陣;
(3)計算加權矩陣W;
(4)假設ANPE=[a0,a1,…,ad-1],特征值排序后為0≤λ0≤…≤λd-1;
(5)yi=ANPETxi,得到變換后的矩陣Y;
(6)使用K均值聚類將Y聚成M個類,進行H次,得到H個聚類成員;
(7)計算每個聚類成員的權值;
(8)對聚類成員使用加權投票進行聚類融合。
3 實驗
3.1 數據集描述
表1列出了來自不同領域的10個時間序列數據集[7]的主要特征。
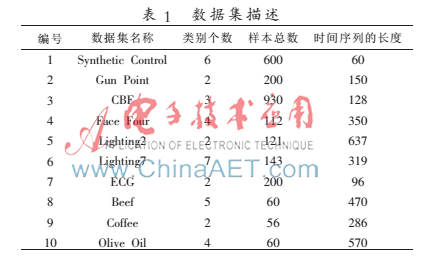
3.2 評價準則
聚類性能用micro-p[6]表示,如式(6)所示。設數據集分為c類{C1,C2,…,Cc},n為樣本個數,ah表示實驗正確分到Ch中的樣本個數,micro-p越大,聚類效果越好。

3.3 性能比較
每一種測試重復10次,記錄平均的micro-p,結果如表2所示。第2列是在原始數據上進行K均值聚類的micro-p,第3、4、5列分別是對PCA、PAA以及NPE降維后的數據進行K均值聚類時最高的micro-p以及相應嵌入空間的維數;第6列給出了對NPE降維后的數據進行聚類融合最高的micro-p以及相應聚類成員個數,用NPEC表示聚類融合算法。

對表2中實驗結果進行配對樣本t檢驗,結果如表3所示。

從表2、表3可以看到,NPEC的平均micro-p為 0.8,高于其他方法。另外,原始數據、PCA、PAA分別與NPEC配對樣本t檢驗的概率p值都小于0.05,說明NPEC的聚類性能顯著地好于這三種方法。
3.4 參數對算法性能的影響
圖1為在Coffee上,將k固定為10,micro-p隨d的變化情況。當d較小時,micro-p較低,聚類性能較差。產生這種情況,一種可能的解釋為數據集中不同的樣本經過NPE映射以后,在低維空間重疊在了一起。隨著d增加,micro-p快速上升,說明本文提出的算法并不需要很高的嵌入維數就可以獲得不錯的聚類效果。

圖2為在Synthetic Control上,將d固定為43, micro-p隨k的變化情況。隨著k的增加,micro-p在一定范圍內波動,說明k對聚類性能的影響較小。

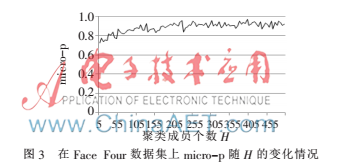
圖3給出在Face Four上,micro-p隨H的變化情況。當H從5增長到100時,micro-p逐漸提高,當H繼續增大時,micro-p保持穩定并在一定范圍內波動。
4 結論
本文提出了一種基于NPE的時間序列聚類融合算法,與已有方法PCA、PAA相比,這種方法更能提高聚類性能。在算法中,如何選擇最優的嵌入維數以及共識函數的設計,值得今后進一步研究。
參考文獻
[1] 陳龍威,孫旭飛.一種基于時間序列分層匹配的騎線車輛檢測方法[J].微型機與應用,2014,33(21):88-91.
[2] 蘇木亞,郭崇慧.基于主成分分析的單變量時間序列聚類方法[J].運籌與管理,2011(6):66-72.
[3] 李海林,郭崇慧,楊麗彬.基于分段聚合時間彎曲距離的時間序列挖掘[J].山東大學學報,2011,41(5):57-62.
[4] He Xiaofei, Cai Deng, Yan Shuicheng, et al. Neighborhood preserving embedding[C]. IEEE International Conference on Computer Vision, 2005:1208-1213.
[5] ROWEIS S T, SAUL L K. Nonlinear dimensionality reduction by locally linear embedding[J]. Science, 2000, 290(5500):2323-2326.
[6] 唐偉,周志華.基于Bagging的選擇性聚類集成[J].軟件學報,2005,16(4):496-502.
[7] Chen Yanping, KEOGH E, et al. The UCR Time Series Classification Archive. www.cs.ucr.edu/~eamonn/time_series_data/.2015.

