摘 要: 對傳統堆排序算法進行分析并做出改進。利用堆的性質降低堆排序過程中的數據比較次數,從而在不提高空間復雜度的前提下改進了堆排序算法的效率。通過理論分析得到改進算法在堆重建過程中的數據比較次數是傳統堆排序算法的一半,即改進算法的時間復雜度的主項系數是傳統算法的1/2。同時,實驗結果表明,改進算法的效率比傳統算法提高了20%左右。
關鍵詞: 堆排序;算法;堆重建;數據比較次數;時間復雜度
0 引言
堆實質是一棵完全二叉樹,其任何一非葉節點滿足性質:(ki≤k2i,ki≤k2i+1)或(ki≥k2i,ki≥k2i+1)(i=1,2,3,4,…,n/2)。利用堆進行排序是一種高效的排序方法,它的時間復雜度為T(n)=2nlog2n+O(n)[1],而且沒有什么最壞情況導致堆排序的運行明顯變慢,同時它的空間復雜性為O(1)[2]。排序算法的優劣衡量標準主要由排序的時間開銷決定,而時間開銷主要由數據的比較次數和數據移動次數決定。理論已經推導出該算法的時間復雜度已經到達了比較排序的時間復雜度下限[3],那么只能降低其時間復雜度的主項系數來提高該算法的效率。參考文獻[3]改進算法與本文算法有些相似之處,但根據參考文獻[3]的實驗數據可知其算法的效率提高了10%左右,而本文中效率提高達到了20%左右。王曉東在《最優堆排序算法》一文中并沒有給出實驗結果,只是從理論上分析了時間復雜度。王珞在《堆排序的推廣改進》一文中雖然效率提高較大,但空間復雜度也提高了,算法也比較復雜。為此,本文在保持傳統算法優點的前提下提出了一種簡單有效的算法來提高效率,并由實驗數據證明算法改進的有效性。
1 問題描述
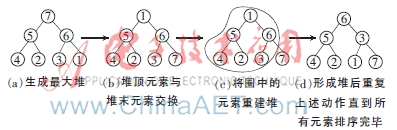
傳統的堆排序分為兩步:(1)根據初始輸入數據,利用堆的調整算法形成初始堆;(2)通過一系列的元素交換和重新調整堆進行排序[2]。排序過程如圖1所示。
在上述過程中不難發現:每次形成最大堆后交換堆頂與堆末元素(記為tail),再逐步做下滑調整重建堆。下滑調整的目的是使大數上浮一層(即使較小的數下滑一層),在該算法中每次下調比較次數是2,移動一次數據。在每次交換數據時,把較小的數放到最頂端,使整個序列又處于比較壞的情況,這無疑增加了許多不必要的數據移動。那么能否為這個被交換的元素(tail)找到它合適的位置再插進去?根據堆的性質可以知道:堆頂的元素被移走后,新的堆頂的元素肯定是它的左右子女中較大的一個。可以不交換數據,先將堆末元素取走,把堆頂元素直接放在堆末元素的位置,在它的子女中找到較大的那個子女上移一層,重復這個動作直到葉節點,這樣在每一層比較中只需要比較一次。
2 算法思路與描述
2.1 改進的算法思路
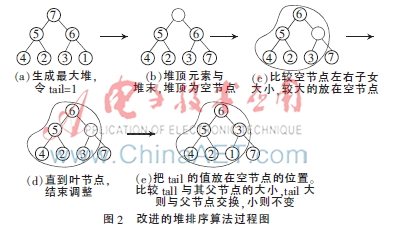
在最大堆生成后,令tail=堆末元素(即先取走堆末元素),堆頂元素放在堆末的位置,則堆頂變為空節點。現在開始把除堆末節點以外的元素重建最大堆,比較空節點左右子女的大小,將較大的那個子女放在空節點的位置,取走的那個子女為新的空節點,重復這個動作直到葉節點。將tail的值填充在空節點。比較原空節點(tail)的值與其父節點的大小,如果父節點較大則不變,反之交換兩個元素的值。
改進的堆排序算法過程如圖2所示。
2.2 tail位置的確定
在上述過程中,需要證明一個問題,即如何在過程最后只比較一次tail的值與父節點的大小就可確定tail的位置。
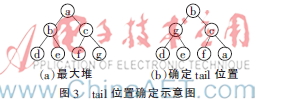
證明過程如下。設圖3(a)中的堆為最大堆,則已知:tail=g,c>g,按照上述規則,a放在g的位置,則a為空節點。現在假設b>c,則b>g,那么b放在圖3(a)中a節點的位置,d、e中較大的元素放在圖3(a)中b節點的位置(設d較大),則現在圖3(a)中d節點的位置為空節點,用tail(即g)的值填充。現在比較d與g的大小,若g大則結果如圖3(b)所示,是符合最大堆的條件的。將假設設為相反的條件,也是同理。所以只需要比較一次tail的值與父節點的大小即可確定tail的位置。
2.3 算法描述
該算法用C++語言描述,核心代碼如下:
template<class T>
void MaxHeap<T>::HeapSort()
{
createMaxHeap(arr);//創建初始堆
T tail=0;
int j=1;
for(int i=currentSize-1;i>=0;i--)
{
if(i<2)
if(heap[0]>heap[1])
{
swap(0,1);
break;
}
int m=0,n=1;
tail=heap[i];//取出堆末元素
heap[i]=heap[0];//堆頂元素放在堆末
while(n+1<i)//重建堆
{
if(heap[n]>heap[n+1])
//找到子女中較大的使其上升
heap[m]=heap[n];
else
{
heap[m]=heap[n+1];
n++;}
m=n;n=2*n+1;//進行下一個子樹的重建
}
if(tail>heap[(m-1)/2])//確定tail的位置
{
heap[m]=heap[(m-1)/2];
heap[(m-1)/2]=temp;
}
else heap[m]=tail;}
};
3 算法復雜度分析與結果對比
3.1 數據移動次數計算
本文中初始堆的建立和數據移動次數與傳統算法一致,所以在此主要是比較數據的比較次數。設二叉樹有n個節點,對應的完全二叉樹的深度為k=log2n+1」。每一次堆重建在二叉樹的每一層都會比較1次,所以要進行k次比較。在整個過程中需要進行n-2次堆的重建,所以數據需要比較k*(n-2)次,每次確定tail位置需要比較一次,共(n-2)次,在最后還需要加上兩個節點的情況,比較2次,所以改進的排序算法數據比較次數為T=nlog2n-2log2n+n。傳統堆排序堆重建的最多比較次數為T=2nlog2n+4n+8[1]。通過兩種算法相比較可知,改進的堆排序算法的比較次數在主項系數上少了一半。
3.2 實驗結果對比
為了證實相應的結論,比較改進的算法與傳統算法之間的效率,在VC6.0環境下用rand()函數產生不同量的隨機數,用QueryPerformanceFrequency()函數獲取算法的計算時間。每組數據是測量的10組數據的平均值,做出兩種算法時間的直方圖,如圖4所示。由圖4可知,提高的效率(時間差/傳統算法時間)分別為18.4%、14.2%、 21.9%、19.0%、24.2%、18.6%、17.1%、15.1%,平均值為18.6%,所以效率提高了20%左右。
4 結論

通過上述分析,傳統的堆排序在堆重建過程中最壞情況下數據比較次數為T=2nlog2n+4n+8,已經達到該類算法時間復雜度數量級下限,因此本文中對算法的改進體現在降低算法中數據比較次數。在理論分析中改進的算法在最壞情況下數據比較次數為T=nlog2n-2log2n+n,可以得到改進算法在主項系數上為傳統算法的一半。通過實驗結果對比可知,改進算法在效率上提高了20%左右,并且該算法在空間復雜性上依舊為O(1),保持了傳統算法的優點,表明該算法的改進是有效的。
參考文獻
[1] 盧開澄.算法與復雜性[M].北京:高等教育出版社,1995.
[2] 殷人昆.數據結構(用面向對象方法與C++語言描述)(第二版)[M].北京:清華大學出版社,2007.
[3] 唐開山.堆排序算法研究[J].紹興文理學院學報,2004,24(10):16-18.

