0引言
盲源信號分離(Blind Source Separation,BSS)是指從觀測到的多源混合信號中分離并恢復出相對獨立的源信號過程。因為對源信號及混合過程知之甚少,無法直接觀測得到混合信號中的有用信息,只有通過盲信號處理手段將它們從混合信號中分離出來,才能實現對所需信號的提取。由于該技術具有在相對寬松的條件實現有用信號的恢復等能力,使之在信號處理領域受到越來越多的關注,并已廣泛應用于通信、語音處理、地震勘探、生物醫學、圖像處理、雷達以及經濟數據分析等領域。
通常的盲源分離算法都不具備對未知信號源個數進行估計的能力,只能在假設信號源的個數已經事先確定的前提下才能進行計算。因此在處理過程中源數目估計對盲分離技術的發展具有重要意義,也是目前必須予以解決的問題。目前有關通信偵查中盲分離源數目估計的專門研究尚不多見,本文研究優化了一種基于累積量算法的源數估計算法,可在無先驗知識的情況下估計出欠定條件下信號源個數。
1信號模型和問題描述
盲源信號分離理論中,混合過程分為線性瞬時混合模型與卷積混合模型兩類。對源信號統計性質的要求還與所采用的盲分離算法有關。本文著重討論線性混合盲信號分離問題情況下信號源數目估計。
存在n個來自信號源的統計獨立n維的信號矢量s1(t),s2(t),…,sn(t),通過m×n的混合矩陣A,線性瞬時混合后得到的m個觀測信號x1(t),x2(t),…,xm(t)。
信號模型為:
![]()
式中:aij是混合矩陣系數;ni為隨機觀測噪聲;矢量和矩陣表達式為:
![]()
式中:n為m×1噪聲矢量。該模型與標準陣列信號處理的觀測信號模型相似,但在盲信號分離中,信號的混合系數并沒有類似陣列信號模型中的波達方向角等先驗信息可以利用。
因此信號源盲分離問題可以描述為計算一個n×m的分離矩陣W,使其輸出y(t)=Wx(t)為對s(t)的一個估計。由于上式中的混合矩陣A和s(t)都未知,因此無法精確辨識源信號各分量的排列順序和能量,這即是盲信號分離問題存在的不確定性問題,一是排列順序的不確定性,即無法了解所抽取的信號應是s(t)中的哪一個分量;二是信號幅度的不確定性,即無法恢復信號波形的真實幅值。由于信息主要包含在信號的波形中,所以這兩種不確定性并不影響盲分離技術的應用。但信號源盲分離的大多數實際問題中,不僅信號源的波形未知,其數目也是未知的。這就無法確定分離矩陣W的維數,從而使計算根本無法進行。故在進行盲分離前,須對信號源數目進行估計。
目前常用的源信號個數估計方法多是基于觀測信號y(t)的協方差矩陣特征分解,易得觀測信號y(t)的協方差矩陣為:
![]()
式中:Rs表示源信號的協方差矩陣,記協方差矩陣Rx特征值為λ1≥λ2≥…≥λn。由于A列滿秩,ARSAT的秩等于k,Rx的特征分解后得到k個按降序排列的主特征值Λs=diag(λ1,λ2,…,λk)和(m-k)均等于σ2的噪聲特征值Λn=diag(λk+1,λk+2,…,λn)=σ2。信源個數就等于k,即m減去相同的最小特征值的個數,僅由觀察其最小特征值重復出現次數就可以確定源信號個數。但是通常觀測信號y(t)的協方差矩陣是未知的,當Rx由一組觀測向量估計得到時,Rx的特征值各不相同的概率幾乎為1,當信噪比比較低時,就很難通過僅觀察特征值來估計源信號個數。
Wax M和Kailath T提出應用信息論中模型AIC和MDL準則估計源信號個數,上述準則都是在標準陣列信號處理中,基于觀測信號均服從高斯分布這一基本假設推導得到的,在標準陣列信號處理模型而源信號非高斯的情形下,H T Wu等給出了源信號個數的啟發性GDE估計,許多國內學者也提出很多新的算法。傳統的盲源分離算法都假設觀測信號數目大于或者等于源信號數目,然而在一些實際應用中會發生觀測信號數目小于源信號數目的情況,稱為欠定盲源分離,即過完備盲源分離。由于混合系統是欠定的,此時混合系統不再可逆,從而不能簡單地通過對混合矩陣求逆得到源信號。因為在混合過程中有信息丟失,即使混合矩陣A已知,也不能完全恢復出信號的獨立成分。
2基于高階累積量的盲信號信源數目估計算法
2.1四階累積量的定義
在實際問題中,一階和二階統計量并不能完全描述信號的統計特性,采用高階統計量的形式不僅可以獲得比二階統計量更好的性能,而且可以解決二階統計量不能解決的很多問題。四階統計量的重要特點是對任何形式下高斯過程的不敏感性,并且在數學形式有很多好的性質,這是二階矩所不具備的,因此可以有效地從高斯過程中提取出非高斯信號或抑制高斯噪聲。這點對于未知譜特性的高斯噪聲情況顯得尤其重要。由于基于高階累積量的相關算法對高斯噪聲嚏盲的,不僅在白高斯噪聲下能正確估計信號源個數,而且對色高斯噪聲和相關高斯噪聲均能有效地抑制,仍能給出一致性的估計。
對于給定隨機變量x1,x2,x3,x4零均值實隨機變量,定義其四階累計量:
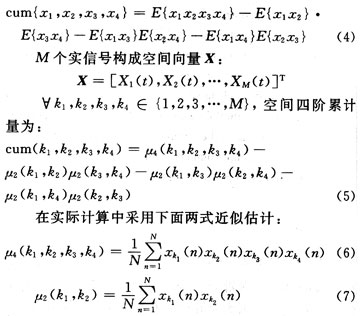
2.2累積量擴展矩陣的構造
在欠定條件下,傳統信源數目估計方法完全失效,通過利用四階累積量的陣列孔徑擴展特性,構造適當的四階累積量矩陣,對協方差矩陣進行擴展,使源信號個數的信息包含于該矩陣中,以估計出多于觀測信號數目的非高斯信號源,借以提高估計算法的性能,突破子空間類算法對入射信號數的限制。
構造的累積量擴維矩陣可以用Kronecker乘積表示,易得實信號模型:
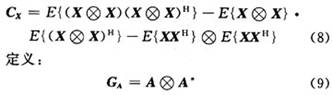
則新信號模型易得:
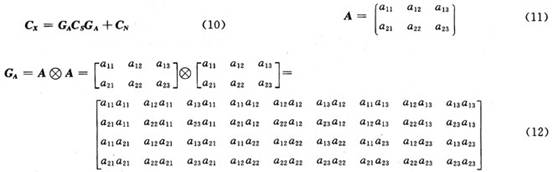
新的混合矩陣中系數位置和原有混合矩陣的位置十分類似,但構成的新矩陣仍然能保持原有信號的獨立性,滿足盲信號分離的基本條件。N個信源,M個通道,M>N,則對GX特征分解后,得到N2大特征值和M2-N2個小特征值。
2.3算法提出
通過結合高階累積量優化過程研究cum-奇異值算法。根據項目條件,在雙通道條件下進行盲源數目的估計。計算過程如下:
設有n個信號(獨立)經過m個通道混合:
(1)采集數據x=[x1(n),x2(n),…,xm(n)]T;
(2)通過高階累積優化構造的四階累積量矩陣CX;
(3)對CX運用cum-奇異值算法得到m2個特征值,并將這些特征值從大到小排列σ1≥σ2≥…≥σm;
(4)主特征值數εδ=k0+1,k0的取值為εδ=γ(kmax)的值,γk=σk+1/σk+2即所求信號源個數。
3仿真實驗
采用2通道3源信號的欠定條件下情形進行仿真實驗,仿真根據項目背景選取的兩組三個獨立信號源分別為AM,FM,BPSK為第一組信號;BPSK,QAM,LFM為第二組信號。其中,AM,FM的載頻為20 MHz,帶寬10 MHz;BPSK和QAM信號的載頻為20 MHz,碼速率為5 MHz;線性調頻信號的初始頻率為20 MHz,帶寬為20 MHz。
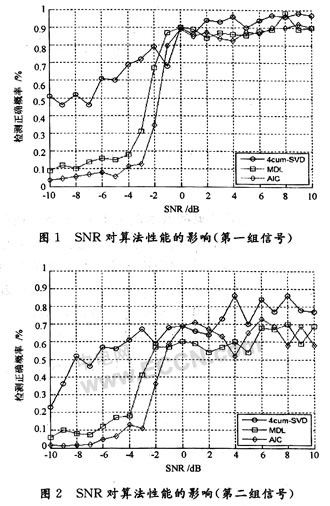
3.1實驗一:信源估計算法性能隨混合信號SNR變化的圖表
任取500點數據,SNR線性變化范圍為-10~10 dB,步長為1 dB,每個SNR點做100次蒙特卡洛仿真。目標個數估計正確率如圖1所示,在欠定條件下優化后,cum-奇異值算法不僅可以估計信源個數,而且隨SNR的遞增,正確估計的概率不斷增大,但同其他經典算法相比,仍然是用時最短的最穩定算法。圖2為第二組信號的正確估計概率。可以看出,該各個算法的性能均明顯有所下降,說明對于不同的信號模型,算法的性能有所不同。盲分離中信源數目估計對模型信號具有一定的要求,不同的混合信號在不同的SNR下正確估計的概率有很大的區別,而通用的方法則不是很多。
3.2實驗二:信源估計算法性能隨混合信號采樣點數變化的圖表
仿真在SNR為8 dB下,數據長度從50~450遞增,步長為50,每個點做100次蒙特卡洛仿真。如圖3所示,四階累積量SVD算法在小樣本條件下性能突出,具有比AIC,MDL算法更高的正確率。但隨快拍數逐漸增加,基于信息論的算法性能開始好轉。圖4說明在同等實驗條件下,不同的信源組合,帶來不同的算法性能。
4結語
本文從盲信號分離的基本假設出發,研究了通信偵查中雙通道盲信號個數的估計方法,通過借鑒陣列信號處理理論,證明了欠定條件下高階累積量優化流程可以應用在信源數目估計的問題,并分別討論了信噪比和采樣點數這兩個參數的變化對優化后算法性能的影響。結果表明,在不同的信號混合情況下,信源算法估計的性能會不同,因為受信源模型、傳播環境等多個因素的影響,會造成性能下降。有關信號模型的多樣性和信源估計算法的局限性及更多數目的情況還有待深入研究,解決方法在后續的修正算法中探討解決。

