文獻標識碼: A
DOI:10.16157/j.issn.0258-7998.2015.07.045
中文引用格式: 宣菊琴,張林垚,吳桂聯,等. 山區分布式電源最優接入容量及位置研究[J].電子技術應用,2015,41(7):162-166.
英文引用格式: Xuan Juqin,Zhang Linyao,Wu Guilian,et al. The study of mountain area distributed generation optimal access capacity and position[J].Application of Electronic Technique,2015,41(7):162-166.
0 引言
分布式電源接入對改善配電網電能質量、提高供電可靠性、降低線路損耗等具有重要作用[1-3]。福建省山區供電網架相對薄弱,系統供電可靠性低,低電壓及線損過高問題較為突出。加大福建省山區分布式電源的開發力度,對于解決上述問題具有重要意義。然而,分布式電源接入容量及位置不同會帶來不同的影響。如何確定合適的接入容量及位置,保證系統更加經濟、可靠地運行,是目前分布式電源接入系統研究的重點內容[4-7]。
分布式電源發電的波動性與隨機性,潛在地增加了分布式電源接入配電網系統的難度。智能算法的產生,為解決優化問題提供了有效途徑。文獻[8]基于線損最小化的目標,針對不同種類分布式電源建立了系統優化模型,利用改進遺傳算法進行模型求解,但遺傳算法容易產生早熟現象,陷入局部最優解;文獻[9]利用改進的粒子群算法對分布式電源的接入進行優化;文獻[10]考慮到系統綜合費用,提出量子微分進化算法對分布電源進行優化配置。但混合后的改進粒子群算法及量子微分進化算法參數較多,編程困難。
螢火蟲算法作為新穎的智能優化算法,其仿生原理簡單,系統參數少,易于編程實現,具有較強的收斂能力及全局尋優能力[11],已成功應用于微網中微源負荷博弈模型的優化求解[12]及分布式風電的優化配置[13]。本文在福建省山區典型配電網供電模式下,以網絡損耗最小為目標,建立了福建山區配電網系統網損目標函數模型,提出利用螢火蟲優化算法進行模型求解,得出了適用于福建省山區配電網分布式電源最優接入容量及位置的尋優方法。
1 分布式電源接入優化模型
分布式電源的接入會對配電網潮流分布產生一定的影響,系統潮流分布的不同直接影響著配電網系統的穩定及經濟性。本文所建優化模型考慮到配電網系統的潮流穩態平衡、節點電壓約束、分布式電源有功功率約束、線路支線功率約束等約束條件。
1.1 潮流分析
分布式電源接入配電網系統模型如圖1所示。

配電網系統中節點i流出的有功及無功功率Pi、Qi如式(1)、式(2)所示:
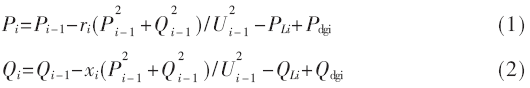
其中,Ui是節點i的節點電壓;ri、xi是節點i與其下一節點所聯的支路電阻及支路電抗;PLi、QLi是節點i的有功負荷及無功負荷;Pdgi、Qdgi為節點i處分布式電源注入的有功功率及無功功率。
根據我國國家電網的相關技術規定,配電網系統中10 kV與380 V電網線路節點電壓不得超過1.07 p.u。因此,考慮到分布式電源接入對線路節點電壓的影響,應保證分布式電源接入系統后,接入點處的線路節點電壓不越限。文獻[5]中考慮到節點電壓越限的情況,給出了分布式電源在電壓不越限下較為實用的最大準入容量的計算方法,在此不再贅述。
1.2 目標函數
分布式電源接入配電網要保證系統更加經濟穩定地運行,接入容量與位置的選取則顯得至關重要。本文所建配電網系統網損目標函數如式(3)所示。
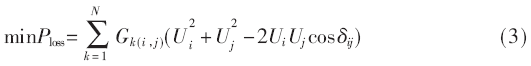
其中,N表示該配電網系統中電網支路的條數, i、j為第k條支路兩端的節點編號,Gk(i,j)則為配電網支路k的電導, δij為節點i、j的電壓相角差。
1.3 模型約束條件
本文所建立的分布式電源最優接入優化模型中,考慮到系統潮流穩定、節點電壓、分布式電源輸出功率及線路功率等約束條件,各等式約束及不等式約束條件如下文所述。
1.3.1 等式約束條件
配電網系統運行穩定時,各節點及線路上的潮流應處于動態穩定的狀態,等式約束條件如式(4)所示。

1.3.2 不等式約束條件
系統不等式約束條件應考慮到分布式電源接入后,保證接入點電壓跌落及越限在合適的范圍內、分布式電源接入容量不超過其最大發電容量、系統線路功率在線路最大承載功率下。各不等式約束方程如下所示。
(1)節點電壓約束

式中:Uimax和Uimin分別為配電網系統中第i個節點電壓的上限及下限值,即在分布式電源接入配電網系統后,接入點電壓不得超過1.07 pu。
(2)DG功率約束

2 螢火蟲算法及優化模型的求解
2.1 螢火蟲算法
劍橋學者Yang通過模擬自然界中螢火蟲的發光特性,于2008年提出了螢火蟲算法。該隨機優化算法的實現過程主要如下所述:
首先對螢火蟲初始化,對不同位置下的螢火蟲進行評價,選出螢火蟲中局部相對吸引度最大的個體和整個螢火蟲中亮度最大的個體;然后螢火蟲向其周圍亮度較高的個體移動,移動后螢火蟲更新自己的位置,同時根據相應的位置更新各自的亮度及吸引度;經過數次移動后,螢火蟲將聚集在亮度最高的位置上。
2.2 分布式電源最優接入容量與位置求解步驟
螢火蟲優化算法中,螢火蟲的亮度與各自的目標函數值有關,目標函數值越大的螢火蟲其亮度越高,相應的吸引度也就越強。在福建省山區分布式電源接入配電網系統優化模型中,本文以福建山區配電網系統網絡損耗最小為目標函數。因此,在螢火蟲優化算法求解過程中,令:

螢火蟲優化算法求解后,尋優的最優值即為對應的配電網系統網絡損耗的最小值。
在福建省山區配電網分布式電源接入容量或位置確定時,確定最優接入位置或容量實現網損最小化的步驟如下所示:
(1)輸入福建省山區配電網系統網損目標函數minPloss=![]() 設置螢火蟲算法中螢火蟲的個數、光吸收系數、最大吸引度、優化迭代次數、系統擾動因子等計算參數。
設置螢火蟲算法中螢火蟲的個數、光吸收系數、最大吸引度、優化迭代次數、系統擾動因子等計算參數。
(2)設置算法中螢火蟲的初始位置集合為X=(x1,x2,…,xn),其中當分布式電源容量確定時,集合X代表分布式電源接入位置集合,xi表示分布式電源接入配電網中的第i個結點,i∈n;當分布式電源接入位置確定時,X代表分布式電源接入容量集合,xi表示分布式電源在配電網中第i個節點的接入容量,i∈n。
(3)計算螢火蟲在不同位置xi時,螢火蟲的最大亮度、吸引度、螢火蟲之間的距離、移動方向等,根據移動的距離及方向對螢火蟲的位置進行更新。
其中:螢火蟲的亮度I表示為:

I0為螢火蟲的最大螢光亮度,γ為光強吸收系數,β0為最大吸引度,xi、xj為螢火蟲i和j所處的位置;α和rand均為擾動隨機參數,用于擴大螢火蟲的搜索空間,避免過早陷入局部最優。
(4)判斷螢火蟲位置xi是否滿足收斂判據 ε。若滿足,則將螢火蟲新位置
ε。若滿足,則將螢火蟲新位置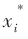 作為最佳位置;若不滿足,則返回步驟(3),繼續改變螢火蟲位置,進行下一輪的位置更新。
作為最佳位置;若不滿足,則返回步驟(3),繼續改變螢火蟲位置,進行下一輪的位置更新。
(5)短路電流校驗,分布式電源接入容量或位置確定后,校驗系統短路點短路電流是否超過線路最大允許短路電流,若不滿足校驗,則返回步驟(2)。
(6)輸出
輸出螢火蟲的最優位置,即在分布式電源接入容量確定時,分布式電源最優的接入位置,或在分布式電源接入位置確定時,分布式電源最優的接入容量。
算法求解流程如圖2所示。

3 算例分析
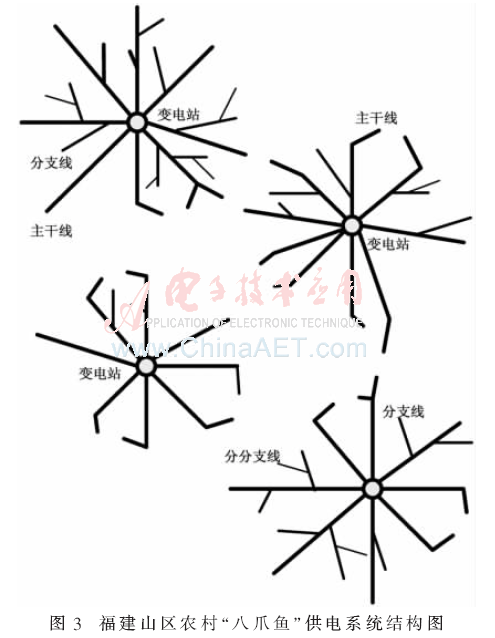
目前,福建省山區農村中壓配電網主要以輻射狀式供電結構為主,已形成“八爪魚”式的電網結構,即一個鄉鎮的中心電源點饋出若干條主線,主線上根據負荷分布饋出若干條小線徑的分支線,分支線上又根據負荷分布饋出若干條更小線徑的分分支線,系統結構如圖3所示。主干線與主干線、分支線與分支線、主干線與分支線之間聯絡極少,幾乎都是輻射狀結構。
為了驗證本文所提螢火蟲優化算法的有效性,取福建省山區配電網“八爪魚”系統結構上的一條中壓饋線進行分析,在該饋線上取出33個節點,各節點分布如圖4所示。
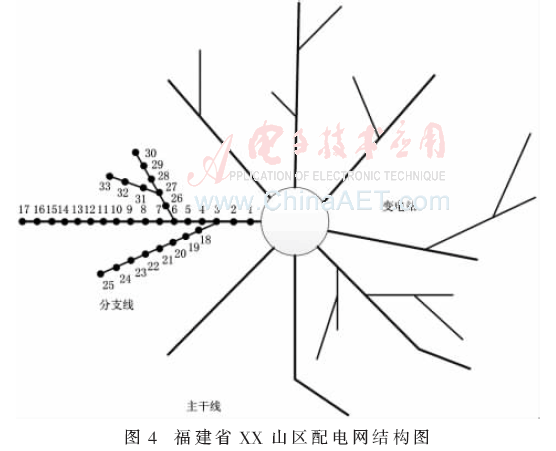
在所分析的供電線路上,系統供電變電站處系統電壓為10.6 kV,線路額定電壓為10.0 kV。該配電網供電線路上共有4條分支線路,最長分支線路(節點1-17)線路長度約10 km。該供電網絡為架空單輻射網絡,主干線路由JKLYJ-240架空線組成,最大輸送容量為10.5 MVA,正常運行時網損率約8%。算例參數如表1和表2所示。

在螢火蟲優化算法中,本文選取200個螢火蟲,設置光強吸收系數γ=7.812 5×10-7,最大吸引度和步長因子分別取為β0=0.9,α=0.8,rand為[0,1]上服從均勻分布的隨機因子,迭代次數為100次。
本次以主干線(節點1-17)為例進行算例分析,從圖4可看出,該供電線路上的分支線路多位于主干線路的前端。因此,主干線路前端的負荷比主干線路后端的負荷多。各主干線路上各節點的最大準入容量如圖5所示。
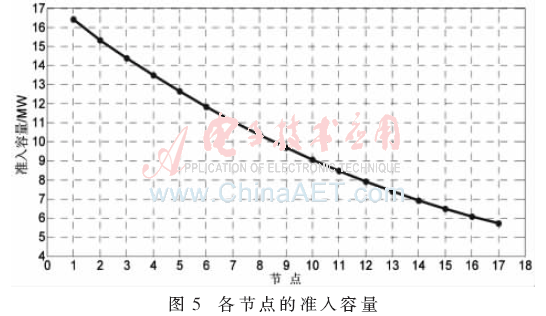
通過計算得主干線末端17節點處的最大準入容量為5.73 MW。從圖5可以看出,越靠近主干線路前端的節點,分布式電源的準入容量就越大,可帶負荷也就越多;反之,在系統主干線路的末端,系統負荷減少,同時為了避免潮流的逆向傳輸,末端分布式電源的最大準入容量相對較小。
當分布式電源位置確定時,通過計算螢火蟲在不同位置時的亮度、吸引度、螢火蟲之間的距離、移動方向等,經過數次尋優,得到了螢火蟲最佳位置點。在螢火蟲算法中,螢火蟲的位置集合即為分布式電源的容量集合。
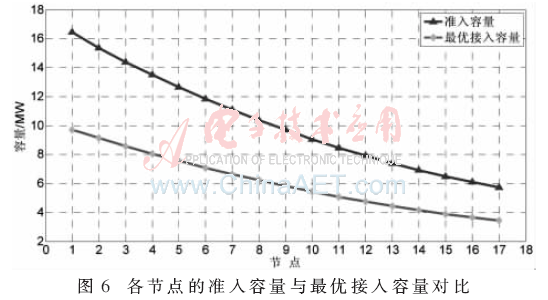
各節點處的最大準入容量與最優接入容量對比如圖6所示。從圖中可看出,分布式電源的最優接入容量同樣沿主干線路逐漸降低,即在主干線路的末端考慮到所帶負荷容量及潮流分布的情況,接入主干線路末端的分布式電源的最優接入容量最小。如果該節點的最優接入容量超過了該節點的最大準入容量,則將準入容量作為該節點的最優接入容量;若該節點的最優接入容量小于其準入容量,則認為已確定的最優接入容量可實現系統網損最小,分布式電源接入后使配電網處于經濟的運行狀態。以主干線路上的末端17節點為例,通過螢火蟲算法的多次尋優,得出17節點最優的接入容量為3.75 MW,低于其最大準入容量5.73 MW。因此, 17節點在接入3.75 MW容量時,滿足節點電壓約束條件,同時在該接入條件下,使得配電網系統網絡損耗最小,提高了系統的經濟性。
4 結論
本文在福建山區配電網典型的“八爪魚”供電模式上,對分布式電源的接入模型進行了研究,同時采用螢火蟲算法進行優化求解。算例結果驗證了螢火蟲算法在分布式電源接入優化求解中的有效性,該算法簡單,易實現。分布式電源最優接入容量與位置的研究,有助于指導福建省山區配電網的規劃,對于山區配電網具有重要的經濟價值和現實意義。
參考文獻
[1] 梁有偉,胡志堅,陳允平.分布式發電及其在電力系統中的應用研究綜述[J].電網技術,2003,27(12):71-75.
[2] 王志群,朱守真,周雙喜,等.分布式發電對配電網電壓分布的影響[J].電力系統自動化,2004,28(16):56-60.
[3] 裴瑋,盛鹍,孔力,等.分布式電源對配網供電電壓質量的影響與改善[J].中國電機工程學報,2008,28(13):152-157.
[4] 劉志昱,黃偉.基于穩態分析和區間層次分析法的分布式電源最佳位置確定方法[J].電網技術,2011,35(11):57-61.
[5] 文升,顧潔,程浩忠,等.分布式電源的注入容量與優化布置的實用方法[J].電力自動化設備,2012,32(10):109-114.
[6] 王建國,楊秀苔.考慮分布式電源接入的新農村電網規劃模型[J].電網技術,2012,36(3):264-268.
[7] 鐘嘉慶,葉治格,盧志剛.分布式發電注入容量與接入位置的優化配置分析[J].電力系統保護與控制,2012,40(7):50-55.
[8] 胡吟,韋鋼,言大偉,等.分布式電源在配電網中的優化配置[J].電力系統保護與控制,2012,40(11):100-105.
[9] 劉波,張焰,楊娜.改進的粒子群優化算法在分布式電源選址和定容中的應用[J].電工技術學報,2008,23(2):103-108.
[10] 于青,劉剛,劉自發,等.基于量子微分進化算法的分布式電源多目標優化規劃[J].電力系統保護與控制,2013,41(14):66-72.
[11] Yang Xinshe.Firefly algorithm for multimodal optimization[C].Proc of the 5th International Conference on Stochastic Algorithm:Foundations and Applications.Berlin:Springer Verlag,2009:169-178.
[12] 王晶,王宗禮,陳駿宇,等.基于螢火蟲優化算法的微網源-荷博弈模型及分析[J].電力系統自動化,2014,38(21):7-12.
[13] 倪健,黃紅程,顧潔,等.基于螢火蟲算法的分布式風電源優化配置[J].華東電力,2014,42(10):2074-2080.

